Как из прямоугольной матрицы сделать квадратную
Действия с матрицами
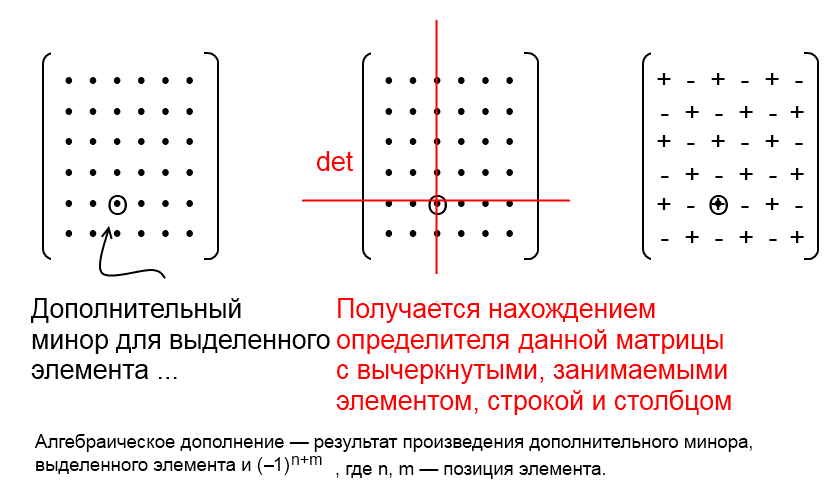
На страницу 1 , 2 След. Последний раз редактировалось LetsGOX Или тут вообще ко-векторы? Все знают, что определитель квадратной матрицы - это объем n-мерного куба, с ориентированными сторонами, заданными векторами в данной матрице С квадратными матрицами тут все понятно, но ведь найти опреелитель неквадттной Например для псевдообъема куба, натянутого на 3 ветора из 4-мерного пространства Итак, к самому нахожению оперделителя неквадратной матрицы Если пользоваться правилом миноров, то получаем набор невычисленных векторов, иначе говоря определитель неквадраной матрицы это не число, а вектор Все бы хорошо, но как понять псевдообщем куба как вектор? Или тут вообще ковекторы?




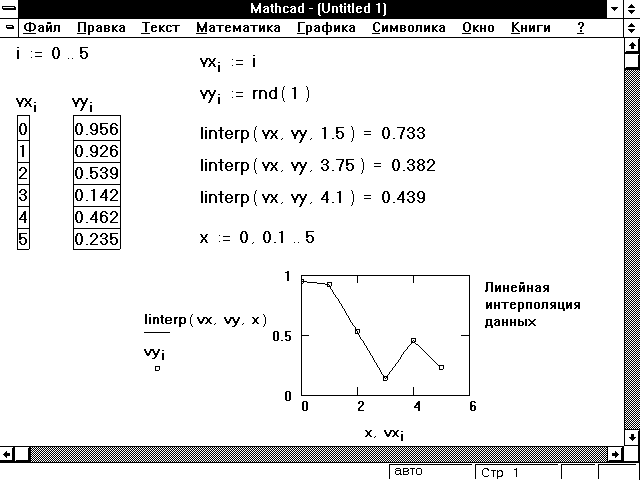




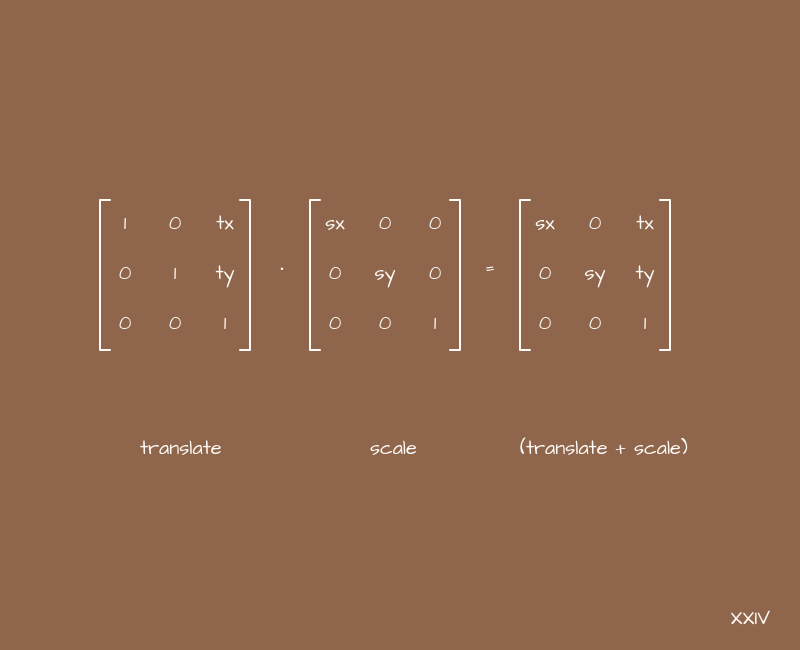
Элементы новой матрицы получаются из элементов старых матриц в соответствии с правилами, проиллюстрированными ниже. Матрицы обладают многими алгебраическими свойствами умножения , присущими обычным числам, за исключением коммутативности. Для квадратных матриц, помимо умножения, может быть введена операция возведения матрицы в степень и обратная матрица. Тогда как матрицы используются для описания, в частности, преобразований математических пространств поворот , отражение , растяжение и другие , произведение матриц будет описывать композицию преобразований. Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что матрицы согласованы. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.





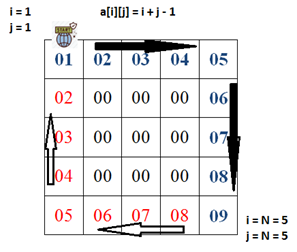


То есть для получения транспонированной матрицы из исходной нужно каждую строчку исходной матрицы записать в виде столбца в том же порядке. Материал из Википедии — свободной энциклопедии. Свойства транспонированных матриц [ править править код ] Дважды транспонированная матрица А равна исходной матрице А. В статье не хватает ссылок на источники см. Информация должна быть проверяема , иначе она может быть удалена.