Почему нельзя подобрать такие натуральные числа a и b

Все дроби в отдельно взятой сумме должны быть различными, а суммы, отличающиеся друг от друга только порядком слагаемых, считаются одним способом. Каждое из слагаемых в правой части можно разложить по тому же принципу сколько угодно раз. Если какие-то знаменатели начнут повторяться в сумме, то можно разложить одну из дробей с повторяющимся знаменателем снова, пока все дроби не станут различными. Таким образом, увеличивая число слагаемых, всякий раз можно добиться того, что в очередном способе каждый знаменатель строго больше любого знаменателя из предыдущих способов.

№ 659. ГДЗ Математика 5 класс Никольский. Помогите подобрать числа

Немного теории, что из себя представляют числа и цифры? Символы выражающие числа называют цифрами 0, 1, 2, То есть, это символы от 0 до 9, из которых можно получить какое-то число. Отсюда и определение, выражения состоящие из цифры называют числами 16, , Числа бывают двух видов:.

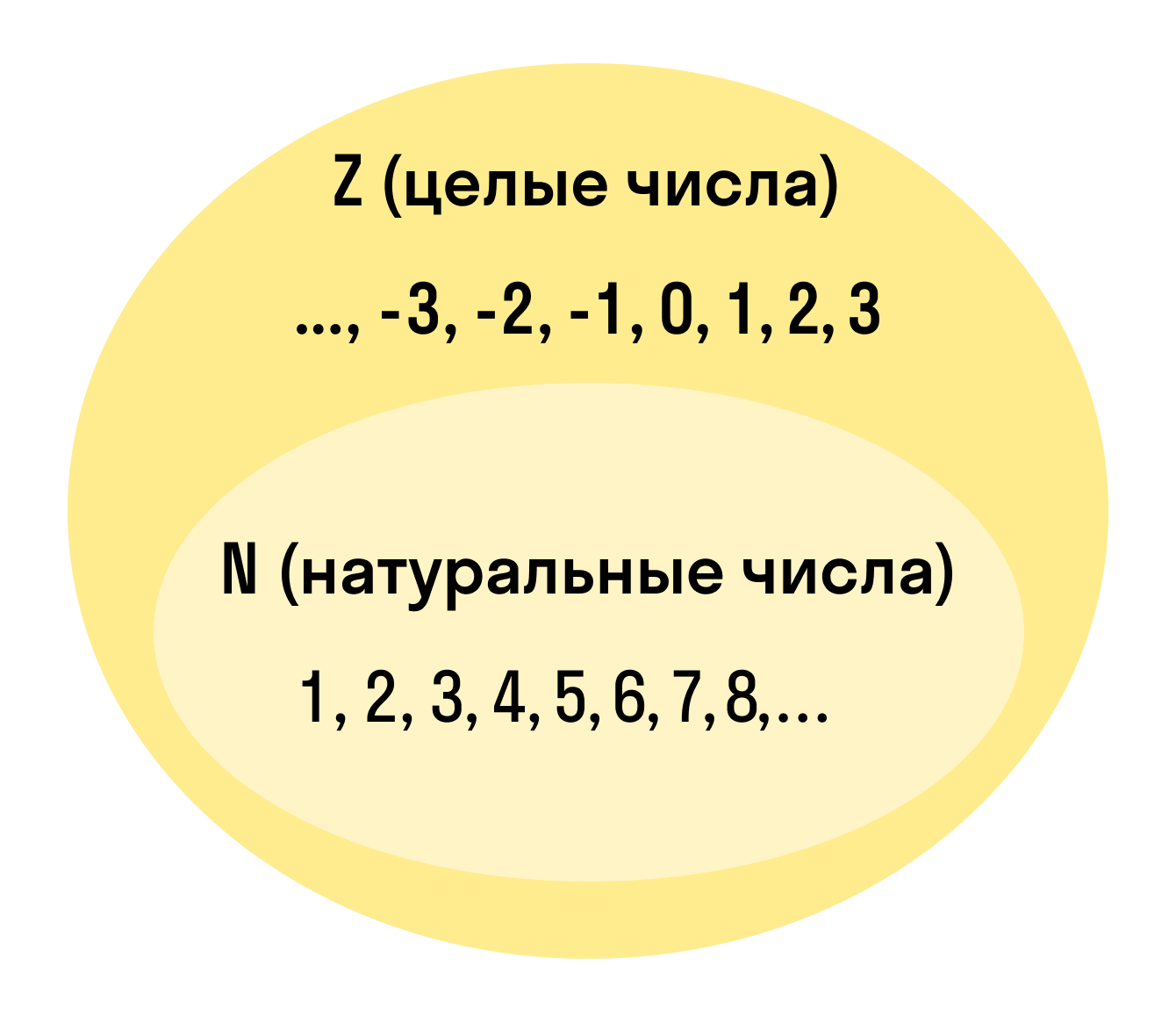
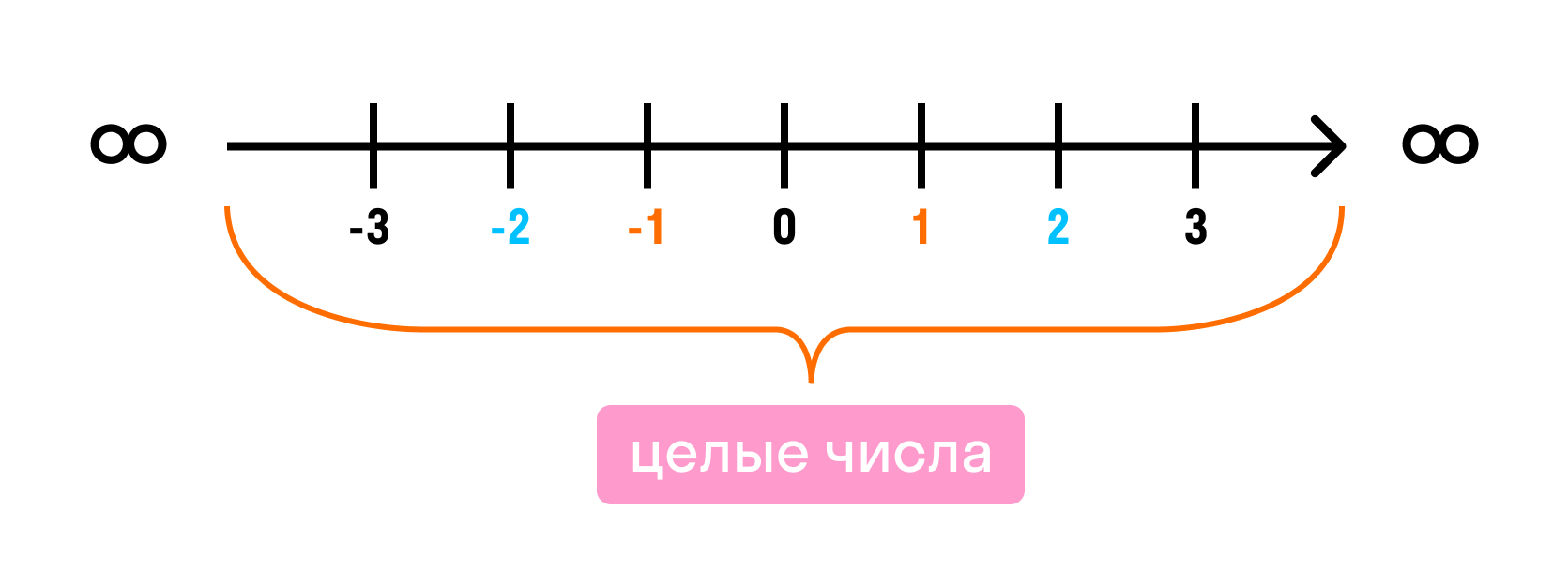
Поскольку мы знаем, что к натуральным числам не относятся отрицательные, дробные и какие-то ещё, кроме положительных целых, получается, что a никак не может быть равным b. Не знаю, может быть это нужно как-то по-другому решать, есть же и второе выражение. Но так как никаких указаний Вы не дали, мой ответ: нет, не верно. Теперь Кью работает в режиме чтения Мы сохранили весь контент, но добавить что-то новое уже нельзя.

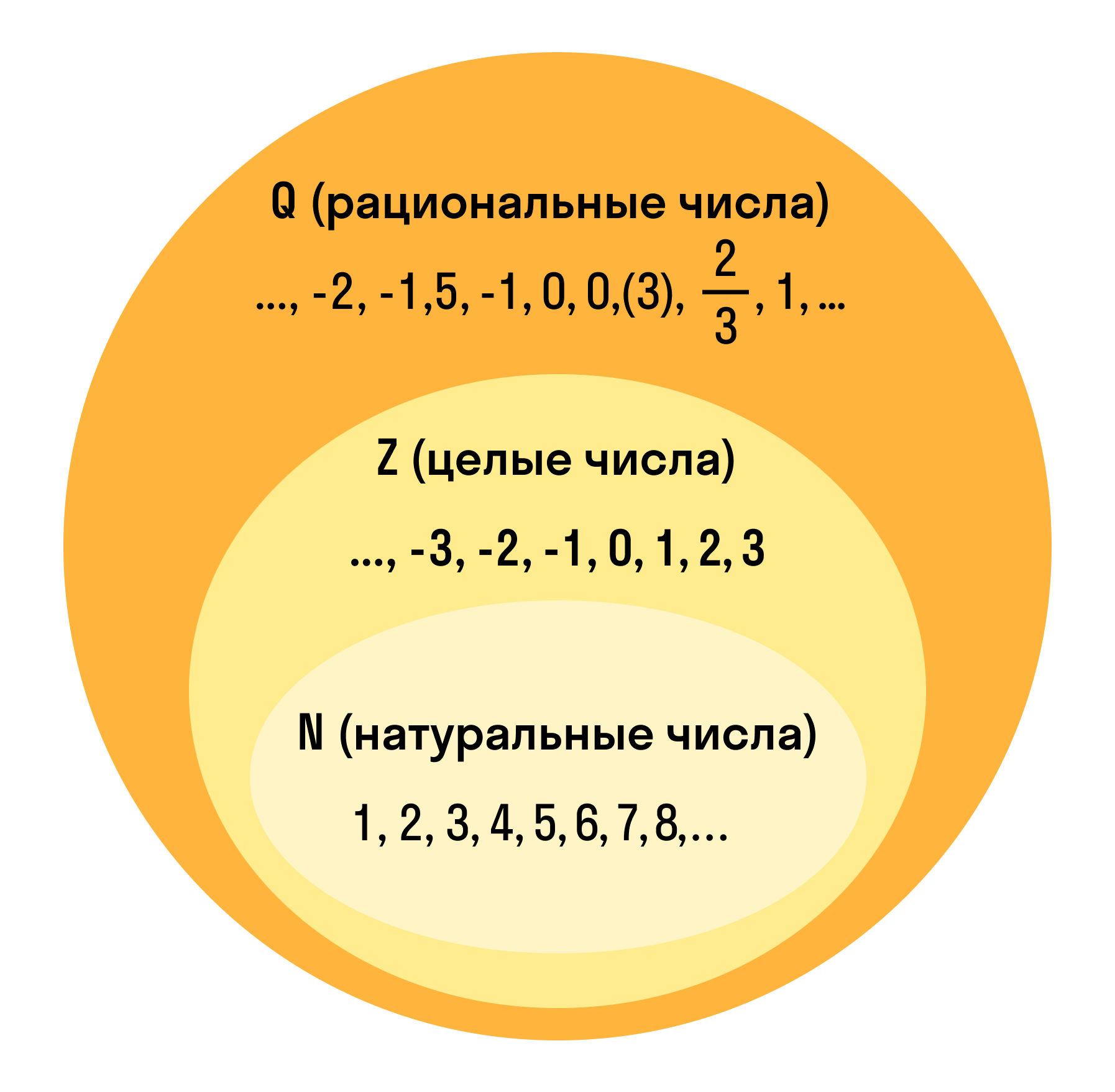
• Если у тебя возникают вопросы, когда в классе, или в учебнике, говорится про натуральные числа, — или о рациональных числах, действительных числах и так далее, — потому что ты не совсем понимаешь, зачем столько названий числам нужно, то ты в правильном месте. Так как все эти разделы о числах проходят в начальной школе, большая часть информации не задерживается в голове, особенно до класса одиннадцатого — на просьбу найти различие между натуральными числами и любыми другими числами, у тебя в голове, скорее всего, будет натуральная пустота.
• Регистрация Вход. Ответы Mail.
• Издатель: Н. Виленкин, В.

	108	Математика невозможна без чисел. Из них состоят примеры, задачи и модели.
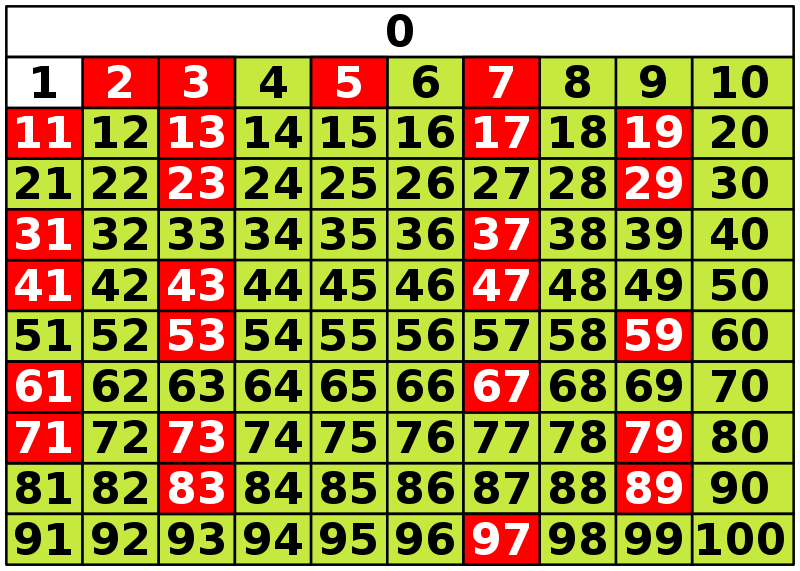
	374	Самое маленькое натуральное число натурального ряда — 1, самого большого числа нет, потому что натуральный ряд можно продолжать бесконечно.
	173	Последовательность всех натуральных чисел, расположенных в порядке возрастания, называется натуральным рядом [2].
	134	Отправить комментарий. В5, задача на числа отношение делимости.
	345	Вычислите объём прямоугольного параллелепипеда, если его рёбра равны: а 18 см, 16 см, 5 см; б 12 см, 45 см, 2 Подробнее Самолёт поднялся в воздух в 14 ч 45 мин и приземлился в 17 ч 10 мин.

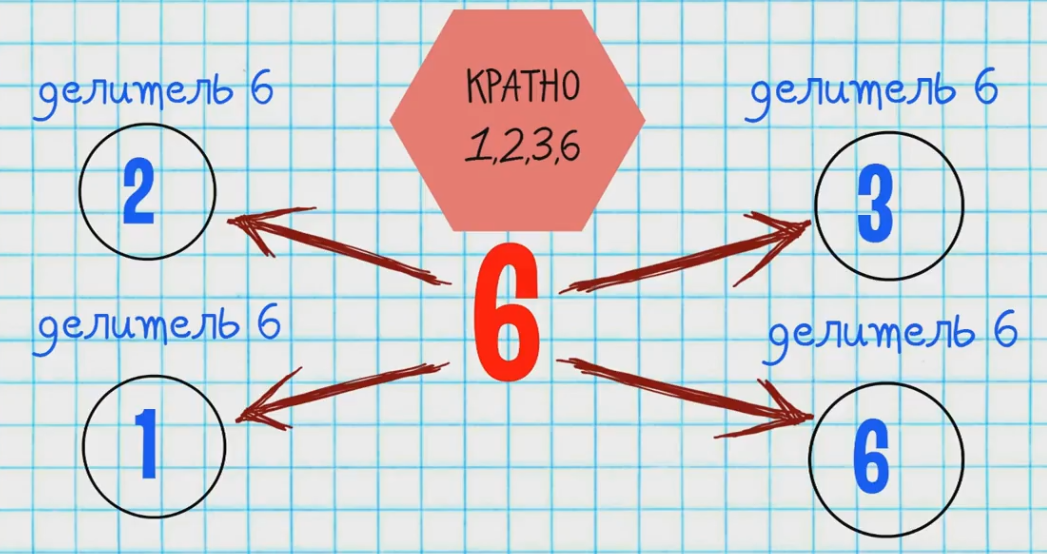
Найти все такие натуральные k , которые можно представить в виде суммы двух взаимно простых чисел, отличных от 1. Эти числа взаимно просты, поскольку из разность равна 4, а 4 взаимно просто с любыми нечётными числами. Таким образом, мы представили в нужном виде все числа, кроме 1, 2, 3, 4 и 6. Нетрудно проверить, что ни одно этих чисел в требуемом виде представить нельзя. Задача Темы:.